Задача
Даны уравнения ax² + bx + c = 0 (1) и – ax² + bx + c (2). Доказать, что если x1 и x2 – соответственно какие-либо корни уравнений (1) и (2), то найдётся такой корень x3 уравнения ½ ax² + bx + c, что либо x1 ≤ x3 ≤ x2, либо x1 ≥ x3 ≥ x2.
Решение
Пусть f(x) = ½ ax² + bx + c.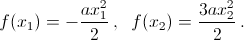 
Эти значения имеют разные знаки, поэтому один из корней трёхчлена расположен между x1 и x2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет