Олимпиадная задача по планиметрии: разделить выпуклую фигуру с дугой и ломаной
Задача
Дана выпуклая фигура, ограниченная дугой A окружности и ломаной ABC так, что дуга и ломаная лежат по разные стороны от хорды AC.
Через середину дуги AC проведите прямую, делящую площадь фигуры пополам.
Решение
Пусть M – середина дуги AC, а N – середина отрезка AC. Если AB = BC, то подойдёт прямая MB. Предположим, что AB < BC. Тогда ломаная BNM делит площадь рассматриваемой фигуры пополам. Построим на отрезке BC такую точку P, что PN || BM. Так как SBNM = SBPM, то отрезок MP также делит площадь нашей фигуры пополам. 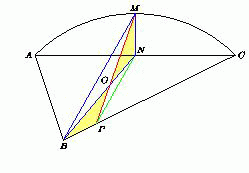
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет