Олимпиадная задача по математике: разбиение класса на группы — минимальное число месяцев
Задача
В классе 16 учеников. Каждый месяц учитель делит класс на две группы.
Какое наименьшее количество месяцев должно пройти, чтобы каждые два ученика в какой-то из месяцев оказались в разных группах?
Решение
Пример. На рисунке показано, как нужно разбивать класс на две группы так, чтобы каждые два ученика в какой-то из четырёх месяцев оказались в разных группах. Каждому ученику соответствует столбец таблицы, а каждому месяцу – её строка. Нуль, стоящий в клетке таблицы, означает, что данный ученик входит в первую группу, а единица означает, что данный ученик входит во вторую группу. Поскольку совпадающих столбцов нет, каждые два ученика хотя бы одни месяц из четырёх находятся в разных группах.
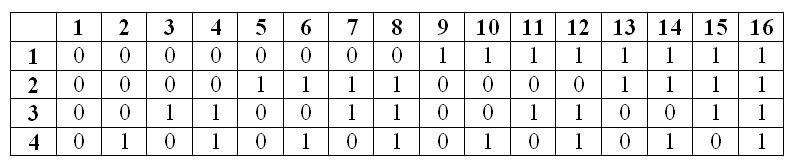
Ответ
4 месяца.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь