Олимпиадная задача по планиметрии для 10–11 классов: угол KJL в треугольнике
Задача
В равностороннем треугольнике ABC провели высоту AH. В треугольнике ABH отметили точку I пересечения биссектрис. В треугольниках ABI, BCI и CAI тоже отметили точки пересечения биссектрис – L, K и J соответственно. Найдите угол KJL.
Решение
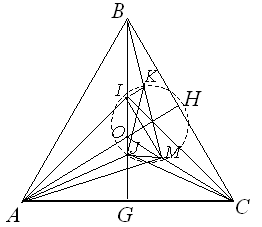
Решение 1: Обозначим через M точку пересечения биссектрис треугольника AHC, а через O – центр треугольника ABC (рис. слева). Точка M из симметрии лежит на биссектрисе угла OBC, то есть точки B, K, M лежат на одной прямой. Из той же симметрии треугольник IMO равнобедренный, то есть ∠IMO = 30°.
∠OAJ = ∠IAJ – ∠IAO = ∠CAJ – ∠CAM = ∠JAM, поэтому AJ и OJ – биссектрисы углов треугольника AOM. Значит, и MJ – тоже биссектриса его угла. Угол между биссектрисами двух углов треугольника выражается через его третий угол (см. зад. 156832). Углы MAO и BCI в треугольниках AOM и CIB равны, следовательно, углы MJO и BKI между их биссектрисами также равны.
Значит, точки I, K, M, J лежат на одной окружности, и ∠BJK = ∠IJK = ∠IMK = ∠OMB – ∠IMO = 45° – 30° = 15°.
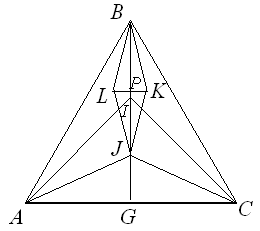
Решение 2: ∠IAC = ∠IAH + ∠HAC = 45°. Поскольку точка I лежит на биссектрисе угла B, AIC – равнобедренный прямоугольный треугольник.
Пусть вписанная окружность треугольника ABI касается стороны BI в точке P. P, очевидно, – середина отрезка KL (рис. справа). Докажем, что P – также середина отрезка BJ. Отсюда следует, что BKJL – ромб и ∠KJL = ∠KBL = 30°.
Пусть AB = 2, тогда 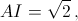 а высота BG треугольника ABC равна
а высота BG треугольника ABC равна 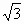 . Как известно (см. зад. 152554),
. Как известно (см. зад. 152554),
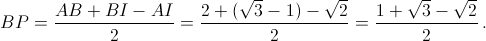
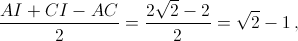 поэтому
поэтому 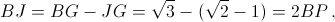 что и требовалось.
что и требовалось.
Ответ
30°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь