Назад

Олимпиадная задача по планиметрии: радиусы вписанных окружностей в треугольниках сложенного квадрата

Задача 216897 • Сложность: 3 • 8-9 класс
Задача

Квадратный лист бумаги согнули по прямой так, что одна из вершин квадрата оказалась на несмежной стороне. При этом образовалось три треугольника. В эти треугольники вписали окружности (см. рис.). Докажите, что радиус одной из этих окружностей равен сумме радиусов двух других.

Авторы:
Штейнгарц Л.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
5
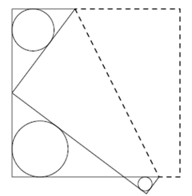
Решение

  Пусть квадрат ABCD перегнули по прямой XY. Обозначим получившиеся точки, как на рисунке.

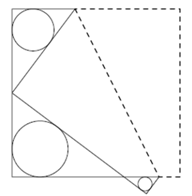
  Диаметры вписанных окружностей треугольниковUDX, UAPиPVYравны соответственно  d1=UD + DX – XU, d2=UA + AP – UP  и d3=PV + VY – PY  (см. задачу156847). Обозначив сторону квадрата черезaи заметив, что  UX = XC  и  VY = YB,  получаем d1+d2–d3=DU+ (a – CX) –CX + PV + BY – PY– (a – DU) – (a – PY – BY) + (a – PV) = 2(DU + BY – CX).   Опустим перпендикулярYKнаCD. ТочкиCиUсимметричны относительноXY, поэтому  XY⊥CU  и  ∠DCU= ∠KYX.  Кроме того,  KY = CD = a.  Следовательно, прямоугольные треугольникиCDUиYKXравны, поэтому  DU = KX = CX – CK = CX – BY.  Это и значит, что  d1+d2–d3= 0.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет