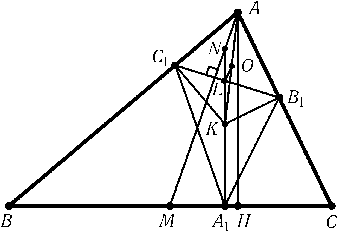
Пусть K — точка Лемуана треугольника ABC; A₁,B₁и C₁ — проекции точки Kна стороны треугольника ABC; L — середина отрезка B₁C₁; N — точка пересечения прямой KLи медианы AM; O — середина отрезка AK(рис.). Точки B₁и C₁лежат на окружности с диаметром AK, поэтому согласно задаче 5.132 OL$\perp$B₁C₁. Кроме того, AN$\perp$B₁C₁(задача 5.133) и O -- середина отрезка AK, а значит, OL — средняя линия треугольника AKNи KL=LN. Следовательно, K — середина отрезка A₁N. Остается заметить, что при гомотетии с центром M, переводящей Nв A, отрезок NA₁переходит в высоту AH.

Ответ задачи отсутствует