Олимпиадная задача по алгебраическим неравенствам и многочленам (9–11
Задача
Докажите неравенство: ![]() + ... +
+ ... + ![]() ≥
≥ 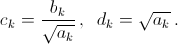 .
.
Значения переменных считаются положительными.
Решение
Решение 1:Заметим, что максимум функции вида f(x) = 2bx – ax² достигается в точке b/a и равен b²/a. Рассмотрим функции fk(x) = 2bkx – akx². Очевидно, что
max (f1(x) + ... + fn(x)) ≤ max f1(x) + ... + max fn(x), что в точности совпадает с доказываемым неравенством.
Решение 2:Это неравенство получается из неравенства Коши – Буняковского (см. задачу 161402) подстановкой 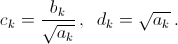
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет