Задание олимпиады: доказательство неравенств Коши и обобщений
Задача
Используя результат задачи 161403, докажите неравенства:
а) ![]() ≤
≤ ![]() неравенство Коши);
неравенство Коши);
б) 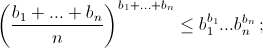 в)
в) 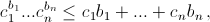 где b1 + ... + bn = 1.
где b1 + ... + bn = 1.
Значения переменных считаются положительными.
Решение
а) Первый способ. Из неравенства Коши для двух чисел (см. задачу 120862) по индукции легко выводится неравенство Коши для n = 2k чисел. Поэтому достаточно доказать, что из неравенства Коши для n чисел следует неравенство Коши для n – 1 числа.
Действительно, согласно неравенству Коши для n чисел
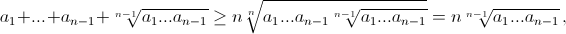 откуда
откуда 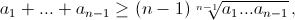 что и требовалось.
что и требовалось.
Второй способ. Пусть a1 + ... + an = n (это не ограничивает общности). Надо доказать, что 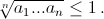 Пусть среди чисел ai есть неравные. Тогда среди них найдутся такие два числа (можно считать, что это a1 и a2), что a1 < 1, a2 > 1. Заменим a1 на c1 = 1, а a2 на
Пусть среди чисел ai есть неравные. Тогда среди них найдутся такие два числа (можно считать, что это a1 и a2), что a1 < 1, a2 > 1. Заменим a1 на c1 = 1, а a2 на
c2 = a1 + a2 – 1. Тогда c1 + c2 + a3 + ... + an по-прежнему равно n, а 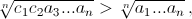 поскольку
поскольку
c1c2 = 1·(a1 + a2 – 1) = a1a2 + (1 – a1)(a2 – 1) > a1a2.
Продолжая эти замены, мы дойдём до набора (1, 1, ..., 1). Следовательно, 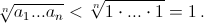
Третий способ. Положим b1 = ... = bn = 1 и применим неравенство из задачи 61403.
Четвёртый способ. Это частный случай неравенства Мюрхеда (см. задачу 161425). б) Положим a1 = ... = an = 1 и применим неравенство из задачи 61403. в) Положим a1 = b1c1, ..., an = bncn и применим неравенство из задачи 61403.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь