Олимпиадная задача по планиметрии и стереометрии о медианах и биссектрисах треугольника

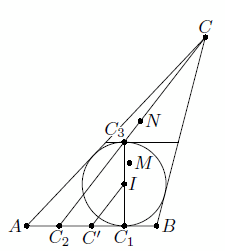
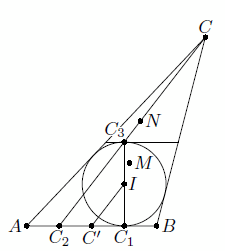
Решение 1:   Пусть C₁ и C₂ – точки касания окружностей ω и ω_C, соответственно вписанной и вневписанной в треугольник ABC, со стороной AB,

а C' – середина этой стороны. Как известно,  C₁C' = C₂C'  (см. задачу 155404). При гомотетии с центром C, переводящей ω_C в ω, точка C₂ переходит в точку C₃ на ω, диаметрально противоположную C₁ (так как касательные к ω в этих точках параллельны; рис. слева). Значит, IC' – средняя линия треугольника C₁C₂C₃, поэтому  C'I || CC₂.  При гомотетии с центром M и коэффициентом –2 точка C' переходит в C, прямая IC' – в параллельную ей прямую СC₂, проходящую через C; следовательно, точка I переходит в точку N, лежащую на CC₂ (аналогично N лежит на отрезках, соединяющих другие вершины с соответствующими точками касания вневписанных окружностей; точка N называется точкой Нагеля треугольника ABC). Значит, N получается из M гомотетией с центром I и коэффициентом 3.

  Перейдём к решению задачи. Пусть  MI=^r/₃.  Тогда точкаNлежит на ω. Пусть для определённости касательная к ω в этой точке пересекает стороныACиBC; тогда ω иCлежат по разные стороны от этой касательной, а значит,  N = C₃.  Так как  IC₃⊥AB,  то и  MI⊥AB  (рис. справа).   Обратно, пусть  AB⊥IM.  Тогда точкаNлежит как на прямойIC₃, так и на прямойCC₂. Поскольку треугольникABCнеравнобедренный, эти прямые различны, а значит,  N = C₃  и  r = IN= 3IM.

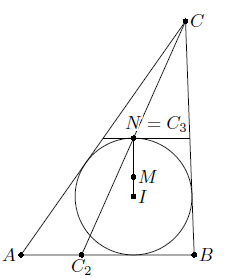
Решение 2:   Пусть  AB ⊥ IM.  Тогда 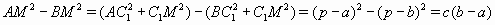     (C₁ – точка касания AB со вписанной окружностью). Пользуясь формулой длины медианы (см. задачу 155267), получаем  AM² = ¹/₉ (2b² + 2c² – a²),  BM² = ¹/₉ (2a² + 2c² – b²),  откуда  c(b – a) = ⅓ (b – a)(a + b),  или  a + b = 3c,  то есть  p = 2c.  Легко показать, что верно и обратное: если  p = 2c,  то  AB ⊥ IM.  Наконец, поскольку

c(IM + r) = 2S_ABM = ⅔ S_ABC = ^2pr/₃,  получаем  IM + r = ^4r/₃,  или  IM = ^r/₃.

  Пусть, наоборот,  MI = ^r/₃.  По известной формуле для момента инерции (см. задачу 157765)

IA² + IB² + IC² = MA² + MB² + MC² + 3MI² = MA² + MB² + MC² + ⅓ r² = ⅓ (a² + b² + c² + r²).  По теореме Пифагора  IA² = r² + (p – a)²;

по формуле Герона 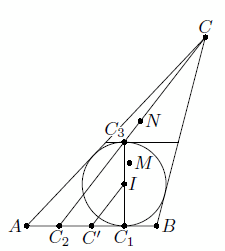    Итак,  ⅓ (a² + b² + c² + r²) = (p – a)² + (p – b)² + (p – c)² + 3r²,  или

  что (после длинных преобразований) приводится к виду

(p – 2a)(p – 2b)(p – 2c) = 0.  Как показано выше, одна из скобок обращается в нуль тогда и только тогда, когда IM перпендикулярно соответствующей стороне.

Ответ задачи отсутствует